ทางเว็บของเรามีบทเรียนดังนี้นะครับ

ท่านสามารถคลิ๊กที่รูปได้เลยครับ

    

     รูป 4.3 ความต่างศักย์และกระแสไฟฟ้า บนตัวต้านทานเมื่อเวลา t ใด ๆ และแผนภาพเฟเซอร์แสดงให้เห็น

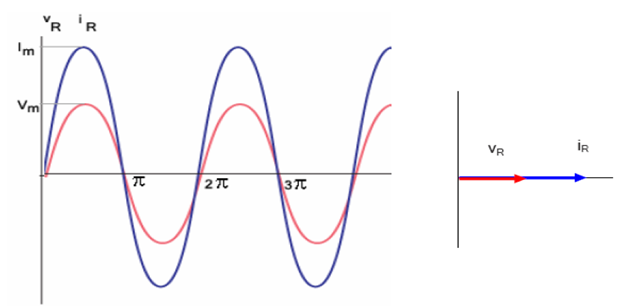
ถึงกระแสมีเฟสตรงกับความต่างศักย์

 

 
                    ความต่างศักย์ไฟฟ้าและปริมาณกระแสไฟฟ้าที่ตกคร่อมตัวต้านทานจะเปลี่ยนไปตามเวลา สามารถ
แสดงเป็นกราฟได้ดังรูป 4.3 ความต่างศักย์ไฟฟ้าและกระแสไฟฟ้าที่ตกคร่อม R จะมีลักษณะที่เรียกว่า
“inphase” หรือมีเฟสตรงกัน เมื่อความต่างศักย์มีค่าสูงสุด กระแสไฟฟ้าก็จะมีค่าสูงสุด และเมื่อความต่างศักย์
มีค่าต่ำสุด กระแสไฟฟ้าก็จะมีค่าต่ำสุดด้วย สมการทั่วไปของกระแสไฟฟ้าสลับที่ไหลผ่านตัวต้านทาน R คือ

        แรงเคลื่อนไฟฟ้าและกระแสไฟฟ้าของวงจรกระแสสลับมีการเปลี่ยนแปลงตลอดเวลาตั้งแต่ 0 ถึง V(m)
หรือ I(m) ค่าแรงเคลื่อนไฟฟ้าและกระแสที่วัดได้จะเป็นค่าที่ขณะใดขณะหนึ่งของเวลา เนื่องจากมีลักษณะเป็น
เส้นโค้งรูป sine ค่าเฉลี่ยของกระแสไฟฟ้าใน 1 รอบจึงมีค่าเป็นศูนย์เพราะขนาดของกระแสในทิศทางที่เป็น
บวกและทิศทางที่เป็นลบมีขนาดเท่ากัน แต่ทิศทางของกระแสที่ไหลสลับไปกลับมาไม่มีผลต่อกำลังไฟฟ้าที่ตก
คร่อมบนอุปกรณ์ไฟฟ้า ตัวอย่างเช่น อุณหภูมิบนตัวต้านทานที่เกิดจากความร้อนเมื่อกระแสไหลผ่านจะแปรผัน
ตามขนาดของกระแสทิศของกระแสไฟฟ้าไม่มีผลแม้แต่อย่างใด
      กำลังไฟฟ้าที่ตกคร่อมบนตัวต้านทาน (R) หาได้จาก (i^2)*R เมื่อ i เป็นกระแสสลับที่เวลาใด ๆ เราอาจคิด
ค่าเฉลี่ยของกระแสแทนค่าของกระแสที่เปลี่ยนแปลงอยู่ตลอดเวลาได้ ค่าโดยเฉลี่ยของกระแสสลับดังกล่าวมี
ชื่อเรียกโดยเฉพาะว่า กระแสยังผล (effective current) โดยนิยามดังนี้

     

     ค่ายังผลของกระแสไฟฟ้าสลับ หมายถึง ค่าของกระแสไฟฟ้าตรงค่าหนึ่ง ซึ่งจะทำให้เกิดพลังงาน
(ความร้อน, แสง, เสียง) บนตัวต้านทานตัวหนึ่งได้เท่ากันในเวลาที่เท่ากัน

                                                   รูป 4.4 การวัดค่ายังผลของกระแสสลับ

 

ในช่วงเวลา dt พลังงานที่เกิดขึ้นบนตัวต้านทานเท่ากับ dW คือ
                             dW = i*R^2*d*t
ต้องการหางานที่ได้จากกระแสไฟฟ้าสลับไหล 1 รอบ ซึ่ง ใช้เวลา T = 2π/ωวินาที

 

อาศัยสูตรตรีโกณมิติ

 

       เมื่อปล่อยกระแสไฟฟ้าค่ายังผล (Ieff) ผ่าน R ตัวเดียวกันในเวลา 1 วินาที เกิดพลังงานบนตัวต้านทานที่
มีค่าเท่ากัน นั่นคือ

 

 

        กระแสไฟฟ้าค่ายังผลบางครั้งเรียกว่าค่าเฉลี่ยกำลังสอง (root mean square current, I(rms) ) เพราะ
ค่าเฉลี่ยของกระแสไฟที่ได้มาจากการนำค่ากระแสไฟฟ้ายกกำลังสองแล้วถอดรากที่สอง

 

 

                                                       รูป 4.5 กราฟแสดง P เฉลี่ย

 

         ในทำนองเดียวกัน แรงเคลื่อนไฟฟ้ากระแสสลับ สามารถหาค่ายังผลของ
แรงเคลื่อนไฟฟ้านี้ได้จาก

     แอมมิเตอร์และโวลต์มิเตอร์ที่ใช้วัดค่าของไฟสลับโดยทั่วไปจะสร้างขึ้นเพื่อวัดค่ายังผลมากกว่าที่จะวัด
ค่าสูงสุด เราสามารถนำค่าจากมิเตอร์ไปหากำลังไฟฟ้าได้จากสูตร  I(rms)^2*R   ได้ โดยตรง ในวงจรไฟฟ้า
กระแสสลับที่ประกอบด้วยตัวต้านทานและแหล่งจ่ายแรงเคลื่อนไฟฟ้าสลับสามารถใช้ค่ายังผลหรือค่าสูงสุดไป
ใช้กับกฎของโอห์มได้โดยตรง

     แรงเคลื่อนไฟฟ้ากระแสสลับที่ใช้ตามบ้านมีค่า 220 โวลต์ เป็นค่ายังผลซึ่งมีแรงเคลื่อนไฟฟ้าสูงสุด
เท่ากับ รากที่สองของ2 × 220 = 311.08 โวลต์

 

2 วงจรที่มีขดลวดเหนี่ยวนำหรือตัวเก็บประจุ

            2.1 วงจรไฟสลับที่มีเฉพาะขดลวดเหนี่ยวนำ

                               รูป 4.6 ความต่างศักย์ที่ตกคร่อมขดลวดเหนี่ยวนำและแผนภาพเฟเซอร์
    

       วงจรที่มีขดลวดเหนี่ยวนำเพียงอย่างเดียว ความต่างศักย์ที่ตกคร่อม L คือ

      เมื่ออินทิเกรตจะได้สมการ i เป็นฟังก์ชันกับเวลา

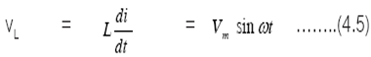
     การอินทิเกรตนี้จะละค่าคงที่ไว้ เพราะสามารถทำให้ค่าคงที่มีค่าเป็นศูนย์ได้โดยการจัดเงื่อนไขเริ่มต้น
ให้เหมาะสม อาศัยตรีโกณมิติ ที่ว่า −cos A = sin (A – 90องศา)

 

                    เมื่อเทียบกับสมการระหว่างความต่างศักย์ที่ตกคร่อมขดลวด(สมการ 4.5) และกระแสที่ไหลผ่าน
ขดลวด (สมการ 4.6 ) จะเห็นว่ามีความต่างเฟสเท่ากับ (ωt-(ωt-π/2 )) =  π/2ความต่างศักย์ที่ตก
คร่อมขดลวดจะมีค่าถึงค่าสูงสุดก่อนกระแสไฟฟ้าที่ไหลผ่านขดลวด กระแสไฟฟ้าจะถึงค่าสูงสุดห่างกันเป็น
ระยะ ¼ ของเวลาการเคลื่อนที่ครบ 1 รอบ นั่นคือเมื่อป้อนแรงดันไฟฟ้ารูปsine ในวงจรที่มีขดลวดเพียงอย่าง
เดียว กระแสไฟฟ้าที่ผ่านขดลวดจะตามหลัง (lag) ความต่างศักย์ที่ตกคร่อมขดลวดอยู่ 90 องศาเสมอ

                   จากสมการ 4.6 ให้ เมื่อ X(L)=ωL คือความต้านของขดลวดเหนี่ยวนำ (Inductive reactance)
มีหน่วยเป็นโอห์มเช่นเดียวกับความต้านทานX(L) จะแปรค่าตามความถี่ของไฟฟ้าสลับ ถ้าความถี่สูงX(L) จะมี
ค่าสูงตามไปด้วย

 
                                  รูป 4.7 กราฟแสดงกระแสที่ผ่านขดลวดตามหลังความต่างศักย์อยู่ 90 องศา

 

 

 

       2.2 วงจรไฟสลับที่มีเฉพาะตัวเก็บประจุ
    วงจรที่ประกอบด้วยตัวเก็บประจุเพียงอย่างเดียว ซึ่งมีสมการแรงเคลื่อนไฟฟ้าในวงจรคือ

 

                                             รูป 4.8 ความต่างศักย์ที่ตกคร่อมตัวเก็บประจุและแผนภาพเฟเซอร์
   กระแสไฟฟ้าในวงจรคือ

         เมื่อเปรียบเทียบสมการ (4.7) และสมการ (4.8) วงจรที่มีตัวเก็บประจุเพียงอย่างเดียวความต่าง
ศักย์ไฟฟ้าที่ตกคร่อมตัวเก็บประจุจะตามหลัง (lag) กระแส ( I ) เป็นมุม 90 องศา
        แผนภาพเฟเซอร์แสดงความต่างเฟสของความต่างศักย์และกระแสไฟฟ้า ดังรูป 4.9 โดย VC จะชี้ไปใน
แนวแกนจินตภาพ (-y) I จะชี้ไปในแนวแกนซึ่งเป็นจำนวนจริง

              รูป 4.9 แสดงกราฟกระแสนำหน้าความต่างศักย์ที่ตกคร่อมตัวเก็บประจุอยู่ 90 องศา

กำหนดให้ XC คือความต้านของตัวเก็บประจุ (Capacitive ractance) = 1 / ωC มีหน่วยเป็น โอหม์

เมื่อ ขนาดกระแสที่ไหลผ่านตัวเก็บประจุมีค่ามากที่สุดคือ Im = Vm / XC

 

ตัวอย่าง 4.4  จากรูป 4.8 ความต่างศักย์ที่ตกคร่อมตัวเก็บประจุขนาด 1 ไมโครฟารัด เขียนเป็นสมการคือ
โวลต์ จงเขีvC = 30 sin 400t ยนสมการแสดงกระแสไฟฟ้าที่ไหลผ่านตัวเก็บประจุ
วิธีทำ

       

         2.3 วงจร RLC แบบอนุกรม

      เมื่อนำตัวต้านทาน ขดลวดเหนี่ยวนำ และตัวเก็บประจุ มาต่ออนุกรม แล้วต่อปลายทั้งสองที่เหลือขอ
งวงจรเข้ากับแหล่งจ่ายไฟสลับ ที่มีแรงเคลื่อนไฟฟ้า

                                                                รูป 4.10 วงจร RLC

         การต่ออนุกรมทำให้กระแสไฟฟ้าขณะใดขณะหนึ่ง(i) ที่ไหลผ่านอุปกรณ์แต่ละตัวมีค่าเท่ากันความต่าง
ศักย์ขณะใดขณะหนึ่งที่ตกคร่อมอุปกรณ์แต่ละตัว หาได้ดังนี้ที่ตัวต้านทาน R

 

 

                                            รูป 4.11 แสดงค่าความต่างศักย์ที่ตกคร่อม R L และ C

           ผลรวมของความต่างศักย์ที่ตกคร่อมอุปกรณ์ทั้งสามชิ้นไม่สามารถรวมกันแบบพีชคณิต เพราะต่างมี
เฟสไม่ตรงกัน จะต้องใช้แผนภาพแสดงเฟสช่วยในการรวม

                       รูป 4.12 แผนภาพแสดงเฟสของความต่างศักย์ที่ตกคร่อมอุปกรณ์แต่ละตัว ในที่นี้ VL > VC
                เพราะกระแสไฟฟ้าที่ไหลผ่านอุปกรณ์แต่ละชิ้นที่เวลาใด ๆ มีค่าเท่ากัน จึงใช้แผนภาพแสดงเฟสของ
ความต่างศักย์ของอุปกรณ์ทั้งสาม โดยเขียนรวมกันเป็นภาพเดียว ดังรูป 4.12 ผลรวม (แบบเวกเตอร์) ของ
ความต่างศักย์ คือค่าความต่างศักย์รวมที่ตกคร่อมทีปลายของอุปกรณ์ ทั้งสามชิ้น

              กำหนดให้อิมพีแดนซ์ของวงจร (บางตำราแปลเป็นไทย ว่าความขัดของวงจร บ้างความต้านทาน
เชิงซ้อนบ้าง )(Impedance, Z) ของวงจร RLC ที่ต่อแบบอนุกรมคือ

มีหน่วยเป็นโอห์ม เช่นเดียวกับความต้านทาน
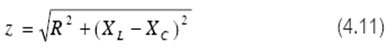
              Z^2 = Resistance^2 + Reactance^2
เขียนสมการ (4.11) ได้ใหม่เป็น
              V(m) = I(m)*Z
              หรือ V(rms) = I(rms)*Z (4.12)

          

                   สมการนี้เป็นการขยายกฎของโอห์ม ให้ใช้ได้กับวงจรกระแสสลับ ในวงจรกระแสตรงกระแสไฟฟ้าที่ไหล
ในวงจรจะขี้นอยู่กับความต้านทานของวงจร แต่ในวงจรกระแสสลับ จะมีค่าความต้านของขดลวดและตัวเก็บ
ประจุซึ่งแปรค่าตามความถี่ของวงจรรวมอยู่ด้วย
จากแผนภาพแสดงเฟส ของความต่างศักย์ในรูป 4.12 ถ้าขจัดตัวร่วม Im ออกไปจะได้แผนภาพแสดง
Impedance ของวงจรดังรูป 4.13

รูป 4.13 แสดงแผนภาพของอิมพีแดนซ์ของวงจร RLC

จากรูปจะเห็นว่า มุมเฟสระหว่างกระแส (แกน x ) กับความต่างศักย์คือ

 

 

                ถ้า XL มีค่ามากกว่า XC ซึ่งมักจะเกิดขึ้นในวงจรที่มีความถี่สูง ๆ มุมเฟสมีค่าเป็นบวกแสดงว่ากระแสที่
เกิดขึ้นวงจรตามหลัง ( lag ) ความต่างศักย์ ถ้า XL มีค่าน้อยกว่า XC มุมเฟสจะติดลบ (หรืออยู่ในควอแดรนท์ที่
4 ) แสดงว่ากระแสไฟฟ้านำหน้า ( lead ) ความต่างศักย์ ถ้า XL เท่ากับ XC มุมเฟสมีค่าเป็นศูนย์ ค่าอิมพีแดนซ์
มีแต่ค่าความต้านทานของตัวต้านทานเพียงอย่างเดียว กระแสในวงจรจะมีค่ามากที่สุด = Vm / R ความถี่ที่ทำ
ให้เกิดสภาวะเช่นนี้ เรียกว่า Resonance frequency

        2.4 การต่อ RLC แบบขนาน

อุปกรณ์ต่าง ๆ เมื่อต่อกันแบบขนานคร่อมกับแหล่งจ่ายไฟกระแสสลับ สามารถวิเคราะห์วงจรได้
เช่นเดียวกับการต่อแบบอนุกรม แต่จะใช้กฎเกี่ยวกับกระแสของเคอร์ชฮอฟ (KCL) ช่วยในการวิเคราะห์

                            รูป 4.17 วงจร RLC ต่อแบบขนาน และแผนภาพสามเหลี่ยมของกระแสในวงจร

                    เพราะตัวต้านทาน ขดลวดและตัวเก็บประจุต่อขนานกันแลัวนำไปต่อกับแหล่งจ่ายไฟสลับ ดังนั้นความ
ต่างศักย์ไฟฟ้าที่คร่อมอุปกรณ์แต่ละชิ้นจึงมีค่าเท่ากัน แต่เฟสของกระแสไฟฟ้าที่ผ่านตัวต้านทาน ขดลวดและ
ตัวเก็บประจุ จะไม่เหมือนกัน การเขียนแผนภาพแสดงเฟสจะใช้กระแสแสดงความต่างเฟส (ไม่เหมือนกับการ
ต่อแบบอนุกรม ซึ่งใช้ ความต่างศักย์แสดงความต่างเฟสในแผนภาพ)

 

กำหนดให้ Impedance ของวงจร RLC เมื่อต่อแบบขนานคือ

จะได้สมการกระแสรวมของวงจร เหมือนกับกรณีต่อแบบอนุกรม คือ
           I = V / Z
มุมเฟสระหว่างกระแสกับความต่างศักย์คือ