
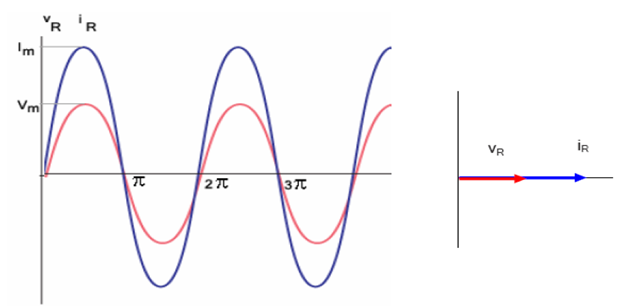
ถึงกระแสมีเฟสตรงกับความต่างศักย์
ความต่างศักย์ไฟฟ้าและปริมาณกระแสไฟฟ้าที่ตกคร่อมตัวต้านทานจะเปลี่ยนไปตามเวลา สามารถ
แสดงเป็นกราฟได้ดังรูป 4.3 ความต่างศักย์ไฟฟ้าและกระแสไฟฟ้าที่ตกคร่อม R จะมีลักษณะที่เรียกว่า
“inphase” หรือมีเฟสตรงกัน เมื่อความต่างศักย์มีค่าสูงสุด กระแสไฟฟ้าก็จะมีค่าสูงสุด และเมื่อความต่างศักย์
มีค่าต่ำสุด กระแสไฟฟ้าก็จะมีค่าต่ำสุดด้วย สมการทั่วไปของกระแสไฟฟ้าสลับที่ไหลผ่านตัวต้านทาน R คือ

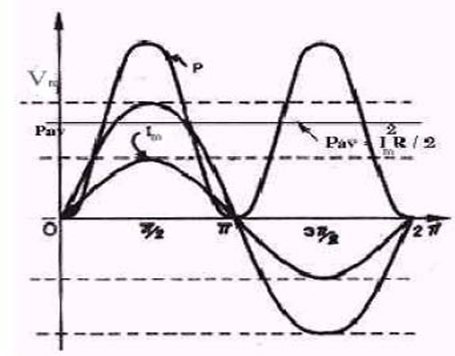
แรงเคลื่อนไฟฟ้าและกระแสไฟฟ้าของวงจรกระแสสลับมีการเปลี่ยนแปลงตลอดเวลาตั้งแต่ 0 ถึง V(m)
หรือ I(m) ค่าแรงเคลื่อนไฟฟ้าและกระแสที่วัดได้จะเป็นค่าที่ขณะใดขณะหนึ่งของเวลา เนื่องจากมีลักษณะเป็น
เส้นโค้งรูป sine ค่าเฉลี่ยของกระแสไฟฟ้าใน 1 รอบจึงมีค่าเป็นศูนย์เพราะขนาดของกระแสในทิศทางที่เป็น
บวกและทิศทางที่เป็นลบมีขนาดเท่ากัน แต่ทิศทางของกระแสที่ไหลสลับไปกลับมาไม่มีผลต่อกำลังไฟฟ้าที่ตก
คร่อมบนอุปกรณ์ไฟฟ้า ตัวอย่างเช่น อุณหภูมิบนตัวต้านทานที่เกิดจากความร้อนเมื่อกระแสไหลผ่านจะแปรผัน
ตามขนาดของกระแสทิศของกระแสไฟฟ้าไม่มีผลแม้แต่อย่างใด
กำลังไฟฟ้าที่ตกคร่อมบนตัวต้านทาน (R) หาได้จาก (i^2)*R เมื่อ i เป็นกระแสสลับที่เวลาใด ๆ เราอาจคิด
ค่าเฉลี่ยของกระแสแทนค่าของกระแสที่เปลี่ยนแปลงอยู่ตลอดเวลาได้ ค่าโดยเฉลี่ยของกระแสสลับดังกล่าวมี
ชื่อเรียกโดยเฉพาะว่า กระแสยังผล (effective current) โดยนิยามดังนี้
ค่ายังผลของกระแสไฟฟ้าสลับ หมายถึง ค่าของกระแสไฟฟ้าตรงค่าหนึ่ง ซึ่งจะทำให้เกิดพลังงาน
(ความร้อน, แสง, เสียง) บนตัวต้านทานตัวหนึ่งได้เท่ากันในเวลาที่เท่ากัน

รูป 4.4 การวัดค่ายังผลของกระแสสลับ
ในช่วงเวลา dt พลังงานที่เกิดขึ้นบนตัวต้านทานเท่ากับ dW คือ
dW = i*R^2*d*t
ต้องการหางานที่ได้จากกระแสไฟฟ้าสลับไหล 1 รอบ ซึ่ง ใช้เวลา T = 2π/ωวินาที
เมื่อปล่อยกระแสไฟฟ้าค่ายังผล (Ieff) ผ่าน R ตัวเดียวกันในเวลา 1 วินาที เกิดพลังงานบนตัวต้านทานที่
มีค่าเท่ากัน นั่นคือ
กระแสไฟฟ้าค่ายังผลบางครั้งเรียกว่าค่าเฉลี่ยกำลังสอง (root mean square current, I(rms) ) เพราะ
ค่าเฉลี่ยของกระแสไฟที่ได้มาจากการนำค่ากระแสไฟฟ้ายกกำลังสองแล้วถอดรากที่สอง
ในทำนองเดียวกัน แรงเคลื่อนไฟฟ้ากระแสสลับ สามารถหาค่ายังผลของ
แรงเคลื่อนไฟฟ้านี้ได้จาก
แอมมิเตอร์และโวลต์มิเตอร์ที่ใช้วัดค่าของไฟสลับโดยทั่วไปจะสร้างขึ้นเพื่อวัดค่ายังผลมากกว่าที่จะวัด
ค่าสูงสุด เราสามารถนำค่าจากมิเตอร์ไปหากำลังไฟฟ้าได้จากสูตร I(rms)^2*R ได้ โดยตรง ในวงจรไฟฟ้า
กระแสสลับที่ประกอบด้วยตัวต้านทานและแหล่งจ่ายแรงเคลื่อนไฟฟ้าสลับสามารถใช้ค่ายังผลหรือค่าสูงสุดไป
ใช้กับกฎของโอห์มได้โดยตรง

แรงเคลื่อนไฟฟ้ากระแสสลับที่ใช้ตามบ้านมีค่า 220 โวลต์ เป็นค่ายังผลซึ่งมีแรงเคลื่อนไฟฟ้าสูงสุด
เท่ากับ รากที่สองของ2 × 220 = 311.08 โวลต์
2 วงจรที่มีขดลวดเหนี่ยวนำหรือตัวเก็บประจุ
2.1 วงจรไฟสลับที่มีเฉพาะขดลวดเหนี่ยวนำ
รูป 4.6 ความต่างศักย์ที่ตกคร่อมขดลวดเหนี่ยวนำและแผนภาพเฟเซอร์
วงจรที่มีขดลวดเหนี่ยวนำเพียงอย่างเดียว ความต่างศักย์ที่ตกคร่อม L คือ
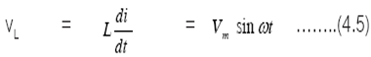
การอินทิเกรตนี้จะละค่าคงที่ไว้ เพราะสามารถทำให้ค่าคงที่มีค่าเป็นศูนย์ได้โดยการจัดเงื่อนไขเริ่มต้น
ให้เหมาะสม อาศัยตรีโกณมิติ ที่ว่า −cos A = sin (A – 90องศา)
เมื่อเทียบกับสมการระหว่างความต่างศักย์ที่ตกคร่อมขดลวด(สมการ 4.5) และกระแสที่ไหลผ่าน
ขดลวด (สมการ 4.6 ) จะเห็นว่ามีความต่างเฟสเท่ากับ (ωt-(ωt-π/2 )) = π/2ความต่างศักย์ที่ตก
คร่อมขดลวดจะมีค่าถึงค่าสูงสุดก่อนกระแสไฟฟ้าที่ไหลผ่านขดลวด กระแสไฟฟ้าจะถึงค่าสูงสุดห่างกันเป็น
ระยะ ¼ ของเวลาการเคลื่อนที่ครบ 1 รอบ นั่นคือเมื่อป้อนแรงดันไฟฟ้ารูปsine ในวงจรที่มีขดลวดเพียงอย่าง
เดียว กระแสไฟฟ้าที่ผ่านขดลวดจะตามหลัง (lag) ความต่างศักย์ที่ตกคร่อมขดลวดอยู่ 90 องศาเสมอ
จากสมการ 4.6 ให้ เมื่อ X(L)=ωL คือความต้านของขดลวดเหนี่ยวนำ (Inductive reactance)
มีหน่วยเป็นโอห์มเช่นเดียวกับความต้านทานX(L) จะแปรค่าตามความถี่ของไฟฟ้าสลับ ถ้าความถี่สูงX(L) จะมี
ค่าสูงตามไปด้วย

รูป 4.7 กราฟแสดงกระแสที่ผ่านขดลวดตามหลังความต่างศักย์อยู่ 90 องศา
2.2 วงจรไฟสลับที่มีเฉพาะตัวเก็บประจุ
วงจรที่ประกอบด้วยตัวเก็บประจุเพียงอย่างเดียว ซึ่งมีสมการแรงเคลื่อนไฟฟ้าในวงจรคือ
รูป 4.8 ความต่างศักย์ที่ตกคร่อมตัวเก็บประจุและแผนภาพเฟเซอร์
กระแสไฟฟ้าในวงจรคือ

เมื่อเปรียบเทียบสมการ (4.7) และสมการ (4.8) วงจรที่มีตัวเก็บประจุเพียงอย่างเดียวความต่าง
ศักย์ไฟฟ้าที่ตกคร่อมตัวเก็บประจุจะตามหลัง (lag) กระแส ( I ) เป็นมุม 90 องศา
แผนภาพเฟเซอร์แสดงความต่างเฟสของความต่างศักย์และกระแสไฟฟ้า ดังรูป 4.9 โดย VC จะชี้ไปใน
แนวแกนจินตภาพ (-y) I จะชี้ไปในแนวแกนซึ่งเป็นจำนวนจริง
รูป 4.9 แสดงกราฟกระแสนำหน้าความต่างศักย์ที่ตกคร่อมตัวเก็บประจุอยู่ 90 องศา
กำหนดให้ XC คือความต้านของตัวเก็บประจุ (Capacitive ractance) = 1 / ωC มีหน่วยเป็น โอหม์

ตัวอย่าง 4.4 จากรูป 4.8 ความต่างศักย์ที่ตกคร่อมตัวเก็บประจุขนาด 1 ไมโครฟารัด เขียนเป็นสมการคือ
โวลต์ จงเขีvC = 30 sin 400t ยนสมการแสดงกระแสไฟฟ้าที่ไหลผ่านตัวเก็บประจุ
วิธีทำ

2.3 วงจร RLC แบบอนุกรม
เมื่อนำตัวต้านทาน ขดลวดเหนี่ยวนำ และตัวเก็บประจุ มาต่ออนุกรม แล้วต่อปลายทั้งสองที่เหลือขอ
งวงจรเข้ากับแหล่งจ่ายไฟสลับ ที่มีแรงเคลื่อนไฟฟ้า
การต่ออนุกรมทำให้กระแสไฟฟ้าขณะใดขณะหนึ่ง(i) ที่ไหลผ่านอุปกรณ์แต่ละตัวมีค่าเท่ากันความต่าง
ศักย์ขณะใดขณะหนึ่งที่ตกคร่อมอุปกรณ์แต่ละตัว หาได้ดังนี้ที่ตัวต้านทาน R
รูป 4.11 แสดงค่าความต่างศักย์ที่ตกคร่อม R L และ C
ผลรวมของความต่างศักย์ที่ตกคร่อมอุปกรณ์ทั้งสามชิ้นไม่สามารถรวมกันแบบพีชคณิต เพราะต่างมี
เฟสไม่ตรงกัน จะต้องใช้แผนภาพแสดงเฟสช่วยในการรวม
รูป 4.12 แผนภาพแสดงเฟสของความต่างศักย์ที่ตกคร่อมอุปกรณ์แต่ละตัว ในที่นี้ VL > VC
เพราะกระแสไฟฟ้าที่ไหลผ่านอุปกรณ์แต่ละชิ้นที่เวลาใด ๆ มีค่าเท่ากัน จึงใช้แผนภาพแสดงเฟสของ
ความต่างศักย์ของอุปกรณ์ทั้งสาม โดยเขียนรวมกันเป็นภาพเดียว ดังรูป 4.12 ผลรวม (แบบเวกเตอร์) ของ
ความต่างศักย์ คือค่าความต่างศักย์รวมที่ตกคร่อมทีปลายของอุปกรณ์ ทั้งสามชิ้น
กำหนดให้อิมพีแดนซ์ของวงจร (บางตำราแปลเป็นไทย ว่าความขัดของวงจร บ้างความต้านทาน
เชิงซ้อนบ้าง )(Impedance, Z) ของวงจร RLC ที่ต่อแบบอนุกรมคือ
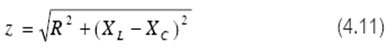
Z^2 = Resistance^2 + Reactance^2
เขียนสมการ (4.11) ได้ใหม่เป็น
V(m) = I(m)*Z
หรือ V(rms) = I(rms)*Z (4.12)
สมการนี้เป็นการขยายกฎของโอห์ม ให้ใช้ได้กับวงจรกระแสสลับ ในวงจรกระแสตรงกระแสไฟฟ้าที่ไหล
ในวงจรจะขี้นอยู่กับความต้านทานของวงจร แต่ในวงจรกระแสสลับ จะมีค่าความต้านของขดลวดและตัวเก็บ
ประจุซึ่งแปรค่าตามความถี่ของวงจรรวมอยู่ด้วย
จากแผนภาพแสดงเฟส ของความต่างศักย์ในรูป 4.12 ถ้าขจัดตัวร่วม Im ออกไปจะได้แผนภาพแสดง
Impedance ของวงจรดังรูป 4.13

จากรูปจะเห็นว่า มุมเฟสระหว่างกระแส (แกน x ) กับความต่างศักย์คือ
ถ้า XL มีค่ามากกว่า XC ซึ่งมักจะเกิดขึ้นในวงจรที่มีความถี่สูง ๆ มุมเฟสมีค่าเป็นบวกแสดงว่ากระแสที่
เกิดขึ้นวงจรตามหลัง ( lag ) ความต่างศักย์ ถ้า XL มีค่าน้อยกว่า XC มุมเฟสจะติดลบ (หรืออยู่ในควอแดรนท์ที่
4 ) แสดงว่ากระแสไฟฟ้านำหน้า ( lead ) ความต่างศักย์ ถ้า XL เท่ากับ XC มุมเฟสมีค่าเป็นศูนย์ ค่าอิมพีแดนซ์
มีแต่ค่าความต้านทานของตัวต้านทานเพียงอย่างเดียว กระแสในวงจรจะมีค่ามากที่สุด = Vm / R ความถี่ที่ทำ
ให้เกิดสภาวะเช่นนี้ เรียกว่า Resonance frequency
2.4 การต่อ RLC แบบขนาน
อุปกรณ์ต่าง ๆ เมื่อต่อกันแบบขนานคร่อมกับแหล่งจ่ายไฟกระแสสลับ สามารถวิเคราะห์วงจรได้
เช่นเดียวกับการต่อแบบอนุกรม แต่จะใช้กฎเกี่ยวกับกระแสของเคอร์ชฮอฟ (KCL) ช่วยในการวิเคราะห์
รูป 4.17 วงจร RLC ต่อแบบขนาน และแผนภาพสามเหลี่ยมของกระแสในวงจร
เพราะตัวต้านทาน ขดลวดและตัวเก็บประจุต่อขนานกันแลัวนำไปต่อกับแหล่งจ่ายไฟสลับ ดังนั้นความ
ต่างศักย์ไฟฟ้าที่คร่อมอุปกรณ์แต่ละชิ้นจึงมีค่าเท่ากัน แต่เฟสของกระแสไฟฟ้าที่ผ่านตัวต้านทาน ขดลวดและ
ตัวเก็บประจุ จะไม่เหมือนกัน การเขียนแผนภาพแสดงเฟสจะใช้กระแสแสดงความต่างเฟส (ไม่เหมือนกับการ
ต่อแบบอนุกรม ซึ่งใช้ ความต่างศักย์แสดงความต่างเฟสในแผนภาพ)
กำหนดให้ Impedance ของวงจร RLC เมื่อต่อแบบขนานคือ
จะได้สมการกระแสรวมของวงจร เหมือนกับกรณีต่อแบบอนุกรม คือ
I = V / Z
มุมเฟสระหว่างกระแสกับความต่างศักย์คือ















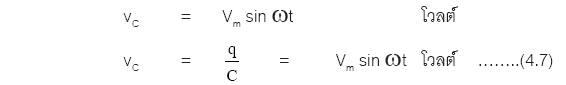
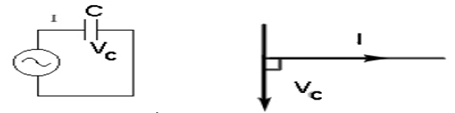



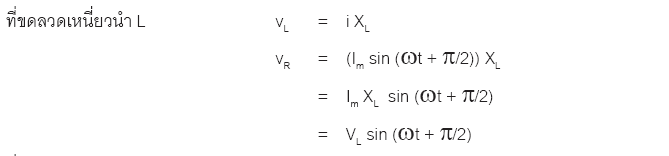



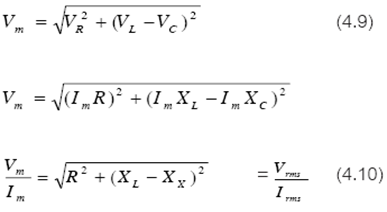







3 comments:
สุดยอดรู้จริง
ขอคุณมากครับ:)
That is the reason consentrate on you will need to unique placement of feet some time before authoring. Will likely be doable to help far more suitable writing in this fashion 검증사이트
Post a Comment